Background

Hybrid quantum systems are highly interesting both from an applied technological viewpoint and for fundamental physics reasons. Technologically speaking, interfacing a future solid state quantum computer capable of local quantum computations with long-distance quantum links formed by optical photons requires a hybrid quantum system, a ‘quantum modem’ interfacing the ‘quantum computer’ with the ‘quantum internet’.

From a fundamental physics viewpoint, an iconic topic of relevance to this project is that of a heavy mechanical oscillator in its quantum ground state. At what mass does the gravitational force become significant and can we observe this? When entangled, a nuclear spin has been proposed as a ‘witness’ to the quantum behaviour of such a system¹.

Physical platform

Nuclear spins in silicon are well-studied, extremely coherent quantum objects. The same applies to high-Q macroscopic mechanical resonators. Thus far these two systems have not been coupled. But a direct coupling mechanism does exist for certain nuclear isotopes: if the nuclear spin is larger than \(1/2\), the nuclear spin couples directly to electric field gradients due to the nuclear quadrupole interaction². Sizeable electric field gradients are caused by microscopic distortions around the atom, such as strain. Through the nuclear quadrupole interaction, dynamic strain will allow driving transitions of the nuclear spin (known as Nuclear Acoustic Resonance)³. In the quantum limit of a resonator this may allow for coherent coupling of a single quantum mechanical vibrational mode, a phonon, and the nuclear spin. We propose to use a nuclear spin of e.g. 73-Ge (spin \(9/2\)) or a group-V donor such as 123-Sb (spin \(7/2\)), implanted in a silicon resonator, for this purpose.

---

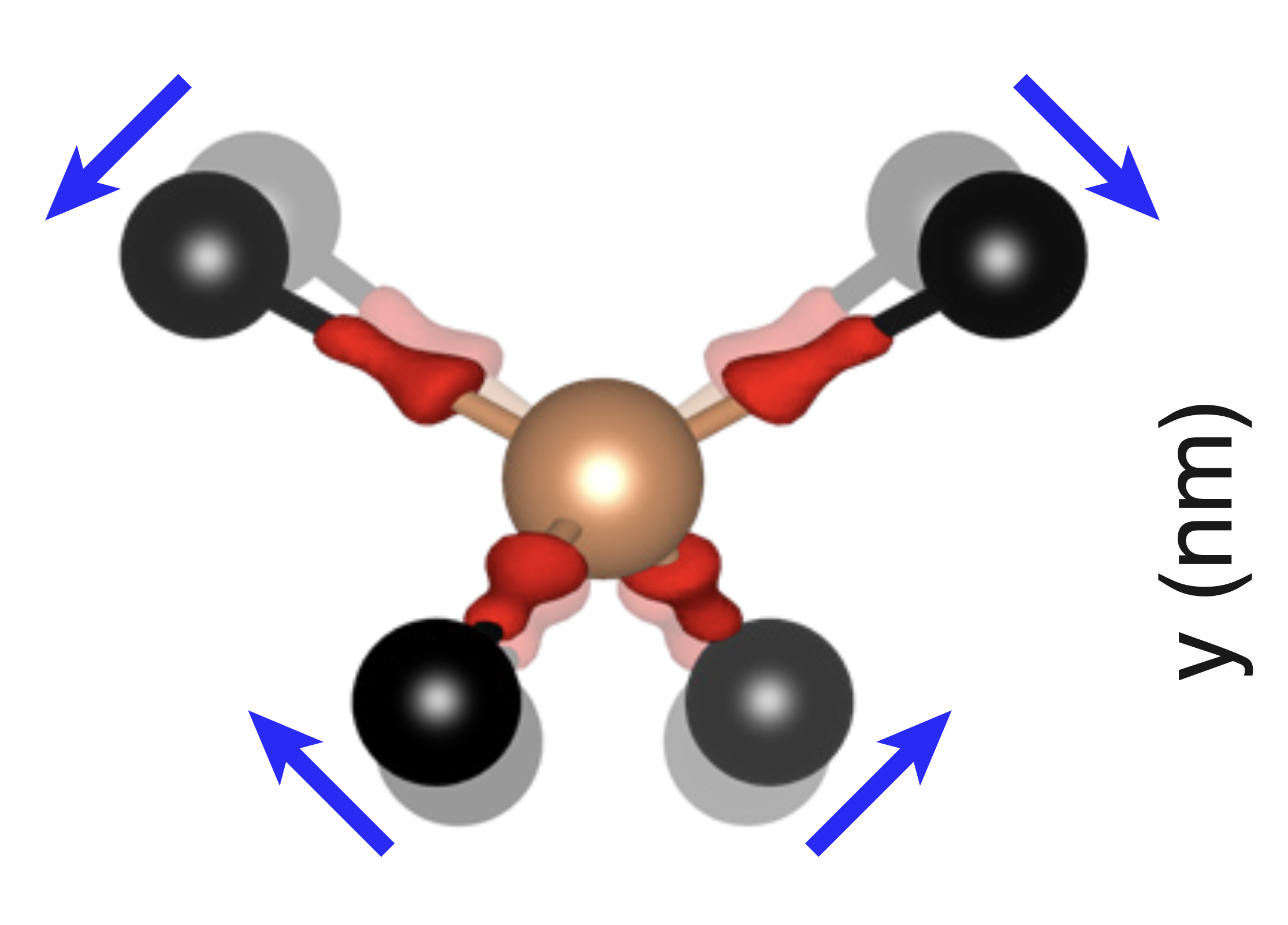High spin nucleus covalently bonded to a silicon lattice (4 silicon atoms shown in black). The larger high spin nucleus locally distorts the lattice. Upon further breaking the lattice symmetry through strain, a significant electric field gradient is present at the nucleus, causing a non-zero nuclear quadrupole interaction term. Dynamical strain in a mechanical resonator may allow for coupling mechanical modes to the nuclear spin. Figure adapted from²

---

Topics for Master thesis project

• Familiarize with basics of nuclear quadrupole interaction, mechanical resonators in the quantum limit, spin-boson coupling Hamiltonian. At a conceptual, small Hamiltonian level.
• Estimate required coupling strengths based on basic Hamiltonian description of the problem.
• Model (using COMSOL) realistic resonator geometry for reaching maximum dynamical strain. Compare different types of resonators (clamped beam, dumb-bell, acoustic membrane, …). Estimate dynamical strain for zero-point motion and use this for comparison to required coupling strength. Assess experimental feasibility
• Optional: consider realistic read-out and detection schemes, in particular integration into on-chip superconducting circuits used in qubit read-out, e.g. through dynamical capacitance of the resonator. Estimate coupling strengths, quality factors etc.
• Optional: Estimate gravitational force between two resonators at a given distance. Estimate maximum noise level of this gravitational force still compatible with quality factors and realistic experimental conditions.

Required Skills

• Self-motivated, independent working style
• Strong background in quantum mechanics and solid-state physics
• Affinity / experience with modelling software and programming
• Affinity with formula based theoretical calculations
• Ability to communicate efficiently with people of a varied background

What we offer

• Workplace, laptop for duration of the project.
• Student assistant contract via RWTH, or equivalent via FZ Jülich contract
• Young, international, dynamical workplace, located on Campus Melaten (Campus- Boulevard 79)
• Exposure to leading research activities in quantum technology

Supervision

• Dr. Vincent Mourik, FZ Jülich, PGI-11 v.mourik@fz-juelich.de
• Dr. Pavel Bushev, FZ Jülich, PGI-13 (FUNQS) p.bushev@fz-juelich.de

References